Encoding FP in Java

is easier than in Go!

`new LambdaWorld<Cadiz>(2018L)`

This presentation is available at

https://gracious-hypatia-aac58b.netlify.com/

(Alt-P for presenter notes)

twitter: @jb9i / github: @jbgi

Jean-Baptiste Giraudeau

heavy French accent
too many years of Java experience
last 3 years as Scala programmer
core contributor of Scalaz and FunctionalJava
Author of Derive4J
Guilty of torturing Java and Scala into confessing their hiden FP abilities.

Thesis of this talk

Typed Functional Programming is the most pratical way to write maintainable, working software.

Not gonna argue this.

Typed Functional Programming require at the minimum a type system that can encode System F.

Java is partialy supportive of this thesis

Java can encode System F, but, out-of-the-box, is missing:

IO effect tracking
Parametricity
Native sum types / GADT
Extensibility other than inheritance
Tail call optimization
Support for Lazy evaluation
HKT (aka. type constructor polymorphism, ie. System Fω)

Encoded in this talk

Desired	Encoded with
[X] IO effect tracking	No side effects + `IO<A>` (from FunctionalJava).
[X] Parametricity	Ignoring everything that can break it.
[X] sum types / GADT	`List<A>{ <X> X cases(X nil, F2<A, List<A>, X> cons);}` (Scott encoding).
[X] Expression Problem solution	Object algebras
[X] Lazy evaluation	`static <A> List<A> lazy(F0<List<A>> as)` (with memoization).
[/] HKT	`List<A>` => `Hk<List<?>, A>` (Unsafe).

Can break Parametricity

hence, in pure code, we completly ignore the existence of:

null
instanceOf / type casts
non-deterministic exceptions
all methods on java.lang.Object

How to prove an encoding is correct?

Hot(t) take: if two types are isormorphic then they are the same.

We ignore bottom values, including null, as per Fast and Loose Reasoning is Morally Correct.

Using cardinality to prove isomorphism

Same cardinality ≃ Isormorphic

Type	Cardinality
`Void`	0
`Unit` / `()`	1
`Boolean`	2
`Either<A, B>`	A + B
`P2<A, B>`	A * B
`F<A, B>`	B^A (need A tests)

What about polymorphic functions??

        interface Id {
          // ∀ a. a -> a
          <A> A f(A a); }
        interface Foo<A, B> {
          // ∀ x. ((a -> x), (b -> x)) -> x
          <X> X f(F<A, X> fa, F<B, X> fb); }
        interface Bar {
          // ∀ a. (a, Either (a, Bool) (b, Bool)) -> (a, a)
          <A> P2<A, A> f(A a, Either<P2<A, Boolean>, P2<B, Boolean>> e); }

We don't know the cardinality of A!

Yoneda to the rescue

If f is a Functor, then:

(∀ x. (a -> x) -> f x) ≃ f a

Equivalences	Step
`∀ x. x -> x`	Introduce unit, `x` ≃ `() -> x`:
`∀ x. (() -> x) -> x`	Introduce `Id` functor (`Id x = x`):
`∀ x. (() -> x) -> Id x`	Apply Yoneda:
`Id ()`	`Id x = x`:
`()`	Q.E.D.

Counting polymorphic types

        interface Id {
          // ∀ a. a -> a
          <A> A f(A a); }
        interface Foo<A, B> {
          // ∀ x. ((a -> x), (b -> x)) -> x
          // ∀ x. (a + b) -> x -> x
          // a + b 
          <X> X f(F<A, X> fa, F<B, X> fb); }
          interface Bar {
            // f :: ∀ a. (a, Either (a, Bool) (b, Bool)) -> (a, a)
            // f a1 Left (a2, b) -> (_, _)
            // f a1 Right (_, b) -> (a1, a1)
            // 16 * 1 = 16.
            <A> P2<A, A> f(A a, Either<P2<A, Boolean>, P2<B, Boolean>> e); }

x^a * x^b = x^(a+b)

Church/Scott encoded Either


interface Either<A, B> {
    
    <X> X match(F<A, X> left, F<B, X> right);
    static <A, B> Either<A, B> Left(A a) {
        return new Either<A, B> {
            <X> X match(F<A, X> left, F<B, X> right) {
                return left.f(a);
            }
        }
    }
    static <A, B> Either<A, B> Right(B b) {
        return new Either<A, B> {
            <X> X match(F<A, X> left, F<B, X> right) {
                return right.f(b);
            }
        }
    }
}

Equivalent using internal visitor

interface Either<A, B> {
    interface Cases<A, B, X> {
        X Left(A leftValue);
        X Right(B rightValue);
    }
    <X> X match(Cases<A, B, X> cases);
    static <A, B> Either<A, B> Left(A a) {
        return new Either<A, B> {
            <X> X match(Cases<A, B, X> cases) {
                return cases.Left(a);
            }
        }
    }
    static <A, B> Either<A, B> Right(B b) {
        return new Either<A, B> {
            <X> X match(Cases<A, B, X> cases) {
                return cases.Right(b);
            }
        }
    }
}

Object are record of functions, right.

Easy extensibility via contravariance

interface These<A, B> {
    interface Cases<A, B, X> extends Either.Cases<A, B, X> {
      X Both(A leftValue, B rightValue);
    }
  
    <X> X match(Cases<A, B, X> cases);
  
    static <A, B> These<A, B> ofEither(Either<A, B> e) {
      return e::match;
    }
}

Adding a new case to Either cases

On Derive4J steroids!!

@Data(flavour=Flavour.FJ)
@Derive(@Instances({ Equal.class, Ord.class, Hash.class, Show.class}))
interface Either<A, B> {
    <X> X match(F<A, X> Left, F<B, X> Right);
    public static void main() {
        Either<Integer, Boolean> l = Eithers.Left(1);
        Either<Integer, Boolean> r = Eithers.Right(true);
    
        Function<Either<Integer, Boolean>, String> toString =
            Eithers.<Integer, String>cases()
                .Left(i -> String.valueOf(i))
                .Right(b -> b ? "true" : "false");
    
        int i = caseOf(l)
                    .Left(identity())
                    .otherwise_(0);
    }
    static <A, B, C> F<Either<A, B>, Either<A, C>> map(F<B, C> f) {
        return Eithers.modRight(f)
    }
}

An annotation processor, compatible with most FP libs

The expression problem

(credit: From Object Algebras to Finally Tagless Interpreters)

Adding new interpreters

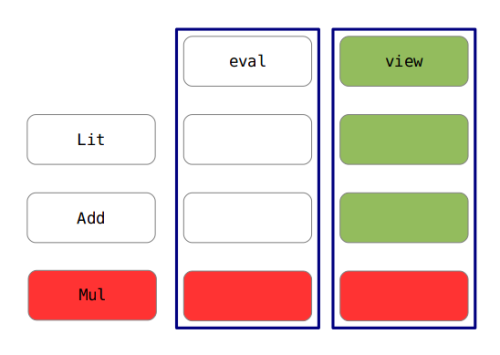
Easy with ADT.

Adding new cases

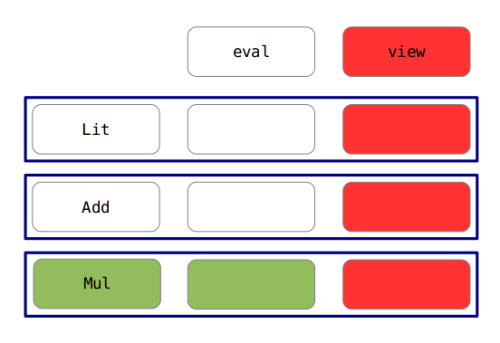
How to do that while reusing existing interpreter without modification?

Object-algebra interfaces

interface ExpAlg<E> {
    E Lit(int lit);
    E Add(E e1, E e2);
}
static <E> E twoPlus3(ExpAlg<E> f) {
    return f.Add(f.Lit(2), f.Lit(3));
}
interface ExpMulAlg<E> extends ExpAlg<E> {
    E Mul(E e1, E e2);
}
static <E> E twoPlus3times5(ExpMulAlg<E> f) {
    return f.Add(f.Lit(2), f.Mul(f.Lit(3), f.Lit(5)));
}
interface ExpMul {
    <E> E withInterpreter(ExpMulAlg<E> f);
}

First compile unit

Interpreters: Object algebras

class EvalExp implements ExpAlg<Integer> {
    @Override
    public final Integer Lit(int lit) {
        return lit;
    }
    @Override
    public final Integer Add(Integer e1, Integer e2) {
        return e1 + e2;
    }
}
class EvalExpMul extends EvalExp implements ExpMulAlg<Integer> {
    @Override
    public final Integer Mul(Integer e1, Integer e2) {
        return e1 * e2;
    }
}

First compile unit

Limitation of final tagless / object-algebra encoding

Programs are a "monolitic" fold.

Manipulating each part as first-class values (initial algebra) simplify some tasks, eg. serialization / delegation to GPU. or just for the simpler API!

Hopefully there is an isomorphism between the two encoding (Lambek’s theorem).

Step 1: Object-algebras are F-algebras

@Data
interface ExpF<E> {
    interface Cases<E, X> {
        X Lit(int lit);
        X Add(E e1, E e2);
    }
    <X> X match(Cases<E, X> cases);
}
interface ExpAlg<E> extends ExpF.Cases<E, E> {}
@Data
interface ExpMulF<E> {
    interface Cases<E, X> extends ExpF.Cases<E, X> {
        X Mul(E e1, E e2);
    }
    <X> X match(Cases<E, X> cases);
}
interface ExpMulAlg<E> extends ExpF.Cases<E, E> {}

data ExpF = Lit Int | Add Int Int

Step 2: Exp as Fixed-point of ExpF

@Data
interface Exp {
    <X> X match(ExpF.Cases<Exp, X> cases);
}
@Data
interface ExpMul {
    <X> X match(ExpMulF.Cases<ExpMulF, X> cases);
    static F<Exp, ExpMul> fromExp() {
        
        ExpMulF.Cases<ExpMul, ExpMul> factory = ExpMuls.factory();
        F<F0<ExpMul>, ExpMul> delay = ExpMuls::lazy;
        return Exps.cata(factory, delay);
    }
}
static <S> Exp ana(F<S, ExpF<S>> coAlg, S seed) { 
    // left as an excercise to the reader ;-)
}

data Exp = Lit Int | Add Exp Exp

On the usefulness of lazy evaluation

aka. call-by-name with sharing.

Allows to implement many operation in the cleanest FP way.

(operation that benefits from TCO (eg. foldLeft) still need while loops).

Eg. Lazy List

public interface List<A> {
  <X> X match(F0<X> Nil,
    @FieldNames({ "head", "tail" }) F2<A, List<A>, X> Cons);
  
  public static <A> F<List<A>, List<A>> filter(F<A, Boolean> p) {
    return Lists.cata(
      Lists::Nil,
      (a, as) -> p.f(a) ? Lists.Cons(a, as) : as, Lists::lazy);
  }
  
  public static <A, B> F<List<A>, List<B>> bind(F<A, List<B>> f) {
    return Lists.cata(
      Lists::Nil,
      (a, as) -> append(as).f(f.f(a)), Lists::lazy);
  }
  
  public static <A> F<List<A>, List<A>> append(List<A> list) {
    return Lists.cata(() -> list, Lists::Cons, Lists::lazy);
  }
  
  public static <A, X> F<List<A>, X> cata(F0<X> Nil, F2<A, X, X> Cons,
    F<F0<X>, X> delay) {
      return new F<List<A>, X>() {
        public X f(List<A> list) {
          return delay.f(() -> list.match(
            Nil, 
            (head, tail) -> Cons.f(head, f(tail))));
        }
      };
    }
  }

Using annotation to define field names

Mandatory fibonacci, using fix point combinators

@Data(flavour = Flavour.FJ)
interface Stream<A> {
  <X> X match(
    @FieldNames({ "head", "tail" }) F2<A, Stream<A>, X> cons);
  default A get(int i) {
    Stream<A> s = this;
    while (0 < i--) {
      s = getTail(s);
    }
    return getHead(s);
  }
  default lazyTail() {
    return lazy(() -> getTail(this))
  }
  default <B, C> zipWith(F2<A, B, C> f, Stream<B> bs) {
    return zipWith(f).f(this, bs);
  }
  static Stream<Long> fibs = fix(fibs ->
    cons(0L, cons(1L, fibs.zipWith((i1, i2) -> i1 + i2, fibs.lazyTail()))),
    Streams::lazy);
  static <A, B, C> F2<Stream<A>, Stream<B>, Stream<C>> 
    zipWith(F2<A, B, C> f) {
      return rec2(rec -> (s1, s2) -> s1.match(
          (a, as) -> s2.match(
              (b, bs) -> cons(f.f(a, b), rec.f(as, bs)))),
          Streams::lazy);
  }
  static <A> A fix(F<A, A> f, F<F0<A>, A> delay) {
    return new Object() {
      final A fix = delay.f(() -> f.f(this.fix));
    }.fix;
  }
  
  static <A, B> F<A, B> rec(F<F<A, B>, F<A, B>> f,
    F<F0<B>, B> delay) {
      return new F<A, B>() {
        final F<A, B> fix = f.f(this);
        public B f(A a) {
          return delay.f(() -> fix.f(a));
        }
      };
  }
  static <A, B, C> F2<A, B, C> rec2(F<F2<A, B, C>, F2<A, B, C>> f,
    F<F0<C>, C> delay) {
      return new F2<A, B, C>() {
        final F2<A, B, C> fix = f.f(this);
        public C f(A a, B b) {
          return delay.f(() -> fix.f(a, b));
        }
      };
  }
}

Scott encoding of an infinite stream

Implementation of lazy constructor

private static final class Lazy<A> implements List<A> {
    private volatile F0<List<A>> expression;
    private List<A> evaluation;
    Lazy(F0<List<A>> list) {
      this.expression = list;
    }
    private synchronized List<A> _evaluate() {
      Lazy<A> lazy = this;
      while (true) {
        F0<List<A>> expr = lazy.expression;
        if (expr == null) {
          evaluation = lazy.evaluation;
          break;
        }
        else {
          List<A> eval = expr.f();
          if (eval instanceof Lazy)
            lazy = (Lazy<A>) eval;
          else {
            evaluation = eval;
            break;
          }
        }
      }
      expression = null;
      return evaluation;
    }
    public <X> X match(F0<X> Nil, F2<A, List<A>, X> Cons) {
      return (this.expression == null ? this.evaluation : _evaluate()).match(Nil, Cons);
    }
  }

Thread-safe, tampolined lazy thunk

Back to F/Object algebras

No HKT => cannot parametrize carrier type. Solutions:

GADT (but no more extensible)
Unsafe HKT encoding

For unsafe encoding: see the Derive4J/HKT project (provide partial safety) and application in Streams à la carte: Extensible Pipelines with Object Algebras

GADT in Java!

abstract class TypeEq<A, B> {
  private TypeEq() {}
  abstract A coerce(B b);
  static <A> TypeEq<A, A> refl() {
        return new TypeEq<A, A>() {
            A coerce(A a) {
                return a;
            }
        };
    }
}
@Data
interface Term<A> {
  interface Cases<A, X> {
    X Lit(int lit, TypeEq<Integer, A> id);
    X Add(Term<Integer> e1, Term<Integer> e2, TypeEq<Integer, A> id);
    X IsZero(Term<Integer> e, TypeEq<Boolean, A> id);
    X If(Term<Boolean> cond, Term<T> then, Term<T> otherwise);
  }
  <X> X match(Cases<A, X> cases);
  public static <T> T eval(final Term<T> term) {
    return Terms.caseOf(term)
        .Lit((i, id) -> id.coerce(i))
        .Add((e1, e2, id) -> id.coerce(eval(e1) + eval(e1)))
        .IsZero((e, id) -> id.coerce(eval(t) == 0))
        .If((cond, then, otherwise) -> eval(cond) ? eval(then) : eval(otherwise));
  }
  static Term<Integer> Lit(int i) {
    return new Term<Integer>() {
        public <X> X match(Cases<Integer, X> cases) {
            return cases.Lit(i, TypeEq.refl());
        }
    };
  }
}

TypeEq: a witness of type equality.

Other nice uses of GADT

single method services:

interface Service {
  <R> IO<R> execute(Command<R> cmd);
}

Almost free (actually initial style) monads (see eg. eventsrc4j).

Pick at initial style monad in Java!

interface Algebra<R, X> extends Pure<R, X> {
  X Read(Long fromSeq, Fold<Event, R> streamFold);
  X Write(Long expectedSeq, List<Event> events,
          TypeEq<WriteResult>, R> resultType);
  <Q> X Bind(StreamAction<Q> q,
             F<Q, StreamAction<R>> f);
}
public interface StreamAction<R> {
  <X> X eval(Algebra<R, X> interpreter);
}

TypeEq avoid the use of continuations

That's all F-olks!

and remember:

"Generics should be the tool of choice for abstracting over types."

Brian Goetz

(and "<? super/extends >" makes you lose that game)

And now let's try

this GADT-based service:

interface Speaker {
  <Answer> Option<Answer> ask(Question<Answer> q);
}